中学生レベルであれば、誰でも確実に答えられるパズルとして、次のようなものがあります。
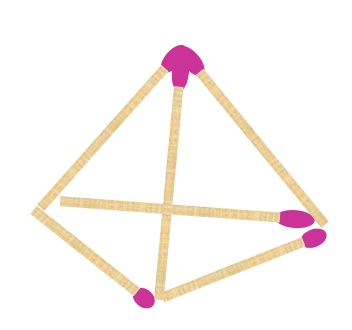
図のように、同じ長さのマッチ棒が６本あります。

このマッチ棒を３本使うと、正三角形が１つできます。
それでは、このマッチ棒を６本使って、正三角形を４つ作ってください。

というのが、このパズルの問題です。

マッチ棒６本から正三角形４つを作るパズルの本質

この問題は、知っている人もいるくらい有名な問題で、問題を見た瞬間に答えが浮かぶ人もいるかもしれません。
このパズルは、心理学の専門家の間では、『洞察問題』というように言われています。
まあ、簡単に言ってしまえば、『ひらめき問題』というとわかりやすいかもしれません。

どうしてこのように言われるのかというと、このパズルを解くときに、最初から正しい解き方を思いつく人が少ないからです。
もちろん知っているという人は除いて、直感的にすぐに答えを導きだせる人もいると思いますが、多くの人は、思いついた解き方をいくつか当てはめてみて、そうした場合にうまくいかない。
でも、気分転換に珈琲でも飲んで別の視点・方法から考えてもやはりうまくいかなかったりします。
ところが、これまでとは全く違う方向から考え始めたとき、「これだ！」とひらめいたりするのです。

つまり、視点を変えてこれまでとは全く違う見方をすることが求められる問題が、『洞察問題』といえるかもしれません。

このパズル問題では、最初に平面で３本のマッチ棒を使って１つの正三角形を作りました。
この平面で考えて攻めるということにこだわってしまうと、いろいろチャレンジしても上手くいきません。

ところが、３次元で考えるという今までとは全く違ったアプローチを思いついたとき、すんなりと立体で考えればいいんだと正解が見えてきます。

ひらめきパズルができるから数学ができるとは限らない

ひらめきパズルができる人は、ＩＱが高いのかとか、想像力があるかとか、分析力があるかというようなことが議論されていますが、パズルを解く才能があるからといって、数学や化学や英語が得意であるとは限りません。

まあ、数学でも幾何の問題はある程度、思いつき・ひらめきといったところもあるのですが、そういったごく一部の問題以外はあまり直接役にはたちません。

学校の勉強や資格試験の勉強といったときに、このパズル問題が直接に役立つというようなことはまずありません。
しかし、こうしたパズルを解く能力というのは、あるに越したことはないのです。

なぜならば、現実に起こってくる問題を解決するためには、固定概念にとらわれず、創造的な思考が必要となってくるからです。
もちろん、このパズル問題ができたからといって、直接数学のテストに関係してくる問題ではないので関係ないでしょう。